not avail
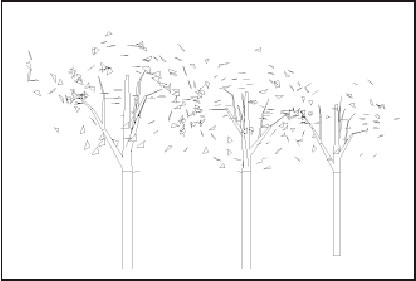
Capita molto spesso che gli utenti di ArchiCAD (ma poi non solo loro) cerchino alberi, non soddisfatti da quelli in loro possesso. Evidentemente questo, di una rappresentazione tridimensionale virtuale di elementi arborei che abbia qualche somiglianza con la rappresentazione manuale consueta, è un problema sentito. Vorrei portare un contributo facendovi fare la conoscenza di Un Albero Molto Speciale, come direbbe Winnie Puh. Questo Albero è Molto Speciale perché adatta la sua rappresentazione tridimensionale alla distanza dalla quale lo stiamo osservando. Ma partiamo dal principio, che è meglio. Chi abbia guardato gli elementi arborei presenti nella libreria fornita con il programma avrà notato come vi sia un solo elemento dotato di una chioma che, volendo, assomiglia abbastanza a come la disegneremmo a mano, avendone una buona. L'elemento di cui parlo è quello che si chiama "albero-3D-a" ("albero-3D-b" è sostanzialmente lo stesso) e non è male. C'è però un problema. A parte il tempo necessario per la sua visualizzazione tridimensionale (problema questo superabile potenziando computer e software in termini di RAM) il vero problema è strutturale, cioè dipende da una caratteristica di ArchiCAD che per certi aspetti può risultare favorevole ma in alcune situazioni diventa negativa. Sto parlando del livello di definizione con cui viene disegnato un elemento: salvo opportuni accorgimenti la definizione con la quale viene rappresentato un elemento è sempre la stessa, indipendentemente dalla distanza che c'è tra l'elemento e la posizione dell'osservatore. Ciò è molto utile perché ci consente di avvicinarci con uno zoom a qualsiasi parte del disegno, controllarla da vicino e magari anche estrapolarla e stamparla. Quando disegnamo a mano cerchiamo di riprodurre una visione il più vicino possibile a quella esperita con gli occhi e quindi in u na prospettiva il livello di definizione si abbassa a mano a mano che aumenta la distanza di ciò che stiamo disegnando, fino ad abbozzare appena gli elementi lontani.

Questo vale per qualsiasi tipo di elemento ma nel caso di elementi arborei l'impatto è più forte: essi infatti hanno bisogno di una definizione geometrica piuttosto articolata per potersi avvicinare a una caratterizzazione "naturale", compatibile con viste ravvicinate. E' ovvio che la stessa definizione non va più bene per distanze più grandi nel qual caso si ottengono macchie scure prodotte dal sovrapporsi di un gran numero di linee in una piccola area di disegno del foglio. Come fare per dare soluzione a questo antipatico problema: una soluzione c'è ed è anche molto semplice: si tratta di adattare il livello di definizione alla distanza di osservazione. Ma come si fa? Tra le Variabili Globali che ci fornisce il GDL, ve ne sono alcune che fanno il caso nostro e sono: K~, L~, M~ che corrispondono alle coordinate cartesiane della posizione dell'osservatore e X~, Y~, Z~ corrispondenti alle coordinate cartesiane della posizione del simbolo. Certamente saprete che le Variabili Globali sono in grado di tenere conto, in modo automatico, delle condizioni generali del contesto progettuale, cioè dei settaggi correnti di ArchiCAD e di alcuni dei suoi elementi utilizzati: ciò significa, per esempio, tenere conto automaticamente della Scala di Disegno, oppure dello spessore del muro nel quale sto inserendo una finestra, oppure ancora dell'altezza del piano corrente. In questo caso ci consentono di riprodurre una logica di disegno, cioè quella per cui il livello di definizione di un elemento decresce all'aumentare della sua distanza dall'osservatore. Vediamo quindi come strutturare una soluzione.
Primo Passo
Far calcolare all'Interprete GDL qual'è la distanza u che separa elemento e osservatore: usando le coordinate cartesiane e il teorema di Pitagora questa istruzione si traduce così:[/jus] x=abs(X~-K~) y=abs(Y~-L~) u=sqr(x*x+y*y)
Secondo Passo
Rendere il livello di definizione dipendente dalla distanza u appena calcolata cosa che realizzeremo usando la Dichiarazione di Salto Condizionato:
if u>90 then 50
if u>60 then 40
if u>30 then 30
dove i tre indirizzi 50, 40, 30 inviano a diverse routine che esprimono un diverso livello di definizione. Ma come far variare il livello di definizione? I modi possono essere i più svariati, questo che segue ne è solo un esempio piuttosto semplice.
Terzo Passo
Stabilire un disegno del fusto e della chioma. Per comodità useremo per il fusto il testo già scritto per l'elemento "albero-3D-a" e ci occuperemo qui solo della chioma. Immaginiamo di disporre una quantità di "foglie" (rappresentate, semplificando, con dei triangoli) su più superfici sferiche concentriche; i raggi delle sfere e l'orientamento delle foglie verranno fatti decidere al caso usando la Funzione Statistica RND.
z=rnd(360)
y=rnd(360)
w=a/4+rnd(a/4)
roty y:rotz z
addx w:roty y:rotz z
poly 3,
0,0, h/20,
0, 0,h/20
Scorrendo il testo a ritroso noteremo l'istruzione poly 3,... che è il triangolo che simula la foglia la cui posizione è definita dalle Trasformazioni di Coordinate espresse nelle due righe precedenti roty y;..., e noteremo ancora che i valori da attribuirsi alle Trasformazioni sono delle variabili il cui valore viene definito più sopra, in modo casuale. Quindi il testo qui sopra costruisce una foglia disponendola in modo casuale sulla chioma. Per costruire più foglie useremo il Ciclo For...Next e, qui sta il punto finalmente, sarà graduando il numero di cicli da compiere, in funzione del livello di definizione, che raggiungeremo il nostro obiettivo.
30:t=150
goto 200
40:t=100
goto 200
50:t=50
200:
addz d+h/2
for i=0 to t
z=rnd(360)
y=rnd(360)
w=a/4+rnd(a/4)
roty y:rotz z
addx w:roty y:rotz z
poly 3, 0,0, h/20,0, 0,h/20
del 5
next i
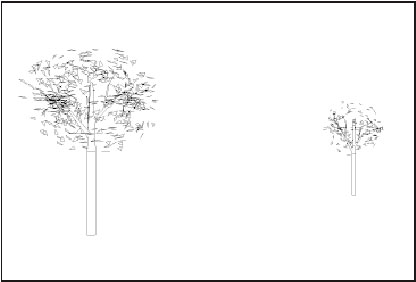
Ai tre indirizzi 30,40,50 corrispondono diversi valori assegnati alla variabile t che poi regola il Ciclo. A questo punto il gioco, sostanzialmente, è fatto e porta ad un ulteriore vantaggio implicito non irrilevante: far disegnare una chioma meno folta per gli alberi lontani non produce solo un disegno più appropriato ma anche un disegno più veloce! Nelle figure 1, 2 e 3 potete verificare il risultato sul "Viale" sugli "Alberi Vicini" e sugli "Alberi Lontani". Ora, quello che abbiamo visto è solo un esempio ma è molto utile per mostrare una logica di procedere nell'affrontare problemi analoghi anche con altri tipi di elementi.